Pythagoras Theorem with Formula, Proof and Examples

The Pythagorean theorem or the Buddhist theorem is a correlation theorem between all three sides of a right triangle in Euclidean geometry. Through this theorem, we can derive the formula of the base, perpendicular, and hypotenuse. It can also be called the Pythagorean theorem. The formula of the Pythagoras theorem and its proof is explained here with examples. This theorem is usually expressed as an equation in the following way-

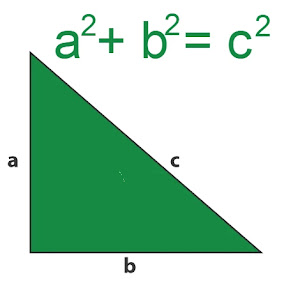
Where "c" is the length of the hypotenuse of a right triangle and "a" and "b" are the lengths of the other two sides. Pythagoras was a Greek mathematician. Traditionally, he is credited with discovering this theorem. However, it is believed that this theorem is dated before them. This theorem is given in the ancient Indian Buddhist Shulbasutra. There is considerable evidence that Babylonian mathematicians also knew this theory. It is also called the "Boudhayan-Pythagoras theorem".

Pythagoras Theorem Statement

According to the Pythagoras theorem "In a right triangle, the square of the hypotenuse of the triangle is equal to the sum of the squares of the other two sides of the triangle". The sides of a right-angled triangle are seen as perpendiculars, bases, and hypotenuse. In these, the hypotenuse is the longest arm, because it is opposite to the angle of 90°. The positive integer value of a right triangle when the square is placed in an equation, also called a Pythagorean triple.

Pythagoras Theorem Formula

If we take the length of the hypotenuse "c" and the length of the other two sides "a" and "b", then the theorem can be expressed as the following equation:

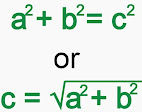
If the value of "c" and one arm is already given and the length of the third arm is to be derived, the following equation can be used:

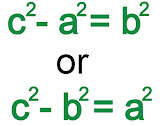
This equation provides a simple relation between the three sides of a right-angled triangle. The generalization of this theorem is called the "cosine rule", with the help of which the length of the third side of any triangle can be calculated if the length of the remaining two sides and the angle between them is measured.

Pythagoras Theorem Proof

This is a theorem that has probably the most evidence compared to other theorems. The law of quadratic reciprocity has also been a competitor to this distinction. In the book, Pythagorean Theorem, composed by Elisha Scott Loomis, 367 pieces of evidence are given.

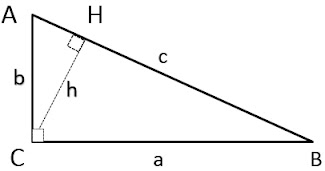
Evidence using a congruent triangle

Let ABC be a right-angled triangle, in which angle C is right-angled, as shown in the figure. We draw a perpendicular to the hypotenuse from point C and the length of that length with arm AB is H. This new triangle ACH is similar to our triangle ABC because they both have right angles (by definition of height) and A is their share of angle. This means that the third angle is also the same in both triangles. On this basis, triangle CBH is also similar to ABC. From these analogies we get two proportions:

Pythagorean Theorem Examples

Example 1: The sides of a triangle are 5cm, 8cm & 9cm. Check if it has a right angle or not.

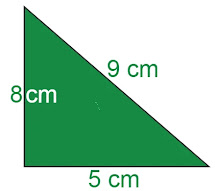
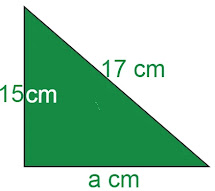
Example 2: The two sides of a right-angled as shown in the figure. Find the third side.

Pythagorean Theorem History

There is debate as to whether the Pythagoras theorem was discovered once or several times, and the date of the first discovery is uncertain, as is the date of the first proof. Mathematical historians of Mesopotamia have concluded that there was widespread use of Pythagoras rule during the Old Babylonian period (20th to 16th century BCE), a thousand years before Pythagoras was born. The history of the theorem can be divided into four parts: knowledge of Pythagoras triangles, knowledge of relations between right-angled triangles, knowledge of relations between adjacent angles, and proofs of the theorem within certain deduction systems.

Written between 2000 and 1786 BCE, Berlin Papyrus 6619 of Middle Kingdom Egypt contains a problem whose solution is the Pythagorean triple 6: 8: 10, but the problem does not refer to a triangle. The Mesopotamian tablet Plumpton 322 was written between 1790 and 1750 BCE during the reign of Hammurabi the Great, which contains several entries relating to the Pythagorean triangles.

In India, the Boudhayan Sulba Sutra, whose dates are dated to between the 8th and 5th centuries BCE, contains a list of Pythagorean trilogies and a description of the Pythagorean theorem, both in the special case of isosceles in both triangles and the general case, As is the Apastamba Sulba Sutra (c. 600 BCE). Van der Waerden believed that this material was "certainly based on earlier traditions". Carl Poyer states that the Pythagoras theorem in Alba-Seventum may have been influenced by ancient Mesopotamian mathematics, but there is no conclusive proof in favour or opposition to this possibility.