Volume of Sphere (Definition, Formula, Derivation and Examples)
The volume of sphere indicates how much capacity the three-dimensional solid has. This means how much money can come to it. The amount of material that can come in a solid indicates its capacity. The shape of the sphere is round and three-dimensional. It consists of three axes. Such as the x-axis, y-axis, and z-axis that define its shape.
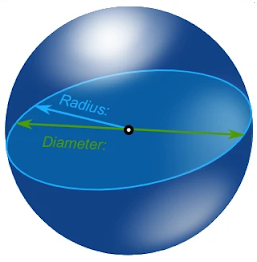
The volume of sphere depends on the diameter and radius of the sphere because if we take the cross-section of the sphere, it is a sphere. The surface area of the sphere is the area of its outer surface. To calculate the volume of a sphere's volume (whose radius is "r"), we have the formula below:
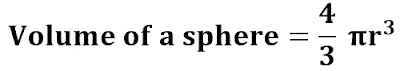
Now we learn to get this formula here and to understand the concept we try to solve some questions.
When you look at a circle and circle, both are circular. A circle can be drawn on paper but cannot be drawn. The difference between the two scenarios is that a circle is a two-dimensional shape and a cycle is a three-dimensional shape, which is why we can measure volume and area.
Volume Of Sphere
A sphere is defined as a solid three-dimensional figure where each of the above points is equal from its center. A fixed distance is called the panel radius and a fixed point is called the center. When the circle is rotated, we will look for a change of scenario. Thus, three-dimensional shape is obtained by rotating a two-dimensional object called a circle
The Archimedes system helps us to determine the volume of a circular object. It states that when a solid object is placed in a container filled with water, the volume of the solid object can be obtained. Because the volume of water flowing from a container is equal to the volume of a circular object.
The volume of Sphere Formula
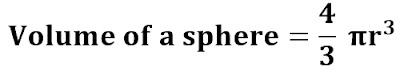
Examples
Example 1: Find the volume of a sphere whose radius is 5 cm?

Example 2: Find the volume of a sphere whose radius is 2 cm?

Example 3: Find the volume of a sphere whose radius is 9 cm?

Example 4: Find the volume of a sphere whose radius is 11 cm?

