Basic Proportionality Theorem (BPT) Proof and Examples

Basic Proportionality Theorem (BPT) is also called Thales Theorem. Because Thales, who introduced the study of geometry in Greece, made an important fact related to similar triangles, "Similar triangles always have the same ratio of the lengths of any two corresponding sides." was proved.

In this article, along with the Basic Proportionality Theorem, we will study the proportionality theorem statement, the basic proportionality theorem proof.

Theorem1: Basic Proportionality Theorem Statement, Basic Proportionality Theorem Proof, Thales Theorem Proof, Thales Theorem Statement-

"A line drawn parallel to one side of a triangle intersects the other two sides, those points divide those sides in equal proportion."

This concept has been introduced in similar triangles. If two triangles are similar to each other then,

  • Corresponding angles of both the triangles are equal
  • Corresponding sides of both the triangles are in proportion to each other

Thus two triangles ΔABC and ΔPQR are similar if,

  • ∠A=∠P, ∠B=∠Q and ∠C=∠R
  • AB/PQ, BC/QR, AC/PR

Proof of Basic Proportionality Theorem

Let us now try to prove the basic proportionality theorem statement

Consider a triangle ΔABC, as shown in the given figure. In this triangle, we draw a line PQ parallel to the side BC of ΔABC and intersect the sides AB and AC in P and Q, respectively.

Basic Proportionality Theorem (BPT)

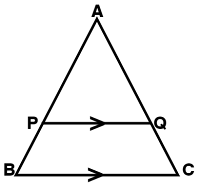
According to the basic proportionality theorem as stated above, we need to prove:

AP/PB = AQ/QC

Construction of Basic Proportionality Theorem

Join the vertex B of ΔABC to Q and the vertex C to P to form the lines BQ and CP and then drop a perpendicular QN to the side AB and also draw PM⊥AC as shown in the figure.

Basic Proportionality Theorem (BPT) Construction

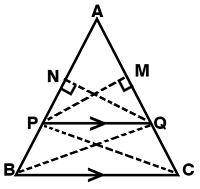
Proof

Now the area of ∆APQ = 1/2 × AP × QN (Since, area of a triangle= 1/2× Base × Height)

Similarly, area of ∆PBQ= 1/2 × PB × QN

area of ∆APQ = 1/2 × AQ × PM

Also,area of ∆QCP = 1/2 × QC × PM ………… (1)

Now, if we find the ratio of the area of triangles ∆APQand ∆PBQ, we have


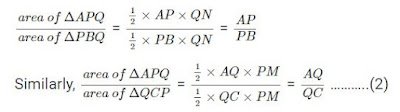
According to the property of triangles, the triangles drawn between the same parallel lines and on the same base have equal areas.

Therefore, we can say that ∆PBQ and QCP have the same area.

area of ∆PBQ = area of ∆QCP   …..(3)

Therefore, from the equations (1), (2) and (3) we can say that,

AP/PB = AQ/QC

Also, ∆ABC and ∆APQ fulfil the conditions for similar triangles, as stated above. Thus, we can say that ∆ABC ~∆APQ.

The MidPoint theorem is a special case of the basic proportionality theorem.

According to the mid-point theorem, a line drawn joining the midpoints of the two sides of a triangle is parallel to the third side.

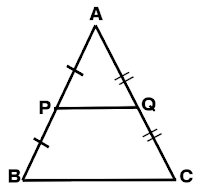
Consider an ∆ABC.

Conclusion

We arrive at the following conclusions from the above theorem:

If P and Q are the mid-points of AB and AC, then PQ || BC. We can state this mathematically as follows:

If P and Q are points on AB and AC such that AP = PB = 1/2 (AB) and AQ = QC = 1/2 (AC), then PQ || BC.

Also, the converse of mid-point theorem is also true which states that the line drawn through the mid-point of a side of a triangle that is parallel to another side, bisects the third side of the triangle.

Hence, the basic proportionality theorem is proved.