Sphere (Definition, Formula and Examples)

That solid spherical object is called a sphere that has only one plane and three dimensions such as (length, width, height). Each point of the plane of the sphere is equally spaced from a fixed point. This point is called the center of the sphere and the distance of any point of the sphere from the center is called the radius of the sphere.

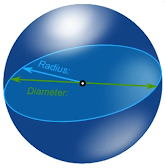
As a circle in a two-dimensional space, a sphere is mathematically defined as a set of points equally separated from a given area, but in a three-dimensional space. This radius is "r", an all-round, radio with a score given less than "r" (or, with a closed ball, less than or equal to it), which is the center of mathematical football. They are also known as radius and field areas respectively. Part of the longest straight line of the ball passes through the center, connecting two points of this space, and the length is doubled; This is the width of both the ball and their ball.

The non-mathematical words "shells" and "balls" are sometimes used, in mathematics, the above distinction is made between space, closed two-dimensional space in a three-dimensional Euclidean area. The difference between football and the field has not always been maintained and the old mathematical references speak as a solid field. This is similar to a plane situation, where the words "circle" and "disk" can also be confused.

Diameter of Sphere

The diameter is a straight line that passes through the center of the sphere and meets the circumference or surface at each end.

Radius of Sphere

The radius of a sphere is a line segment between the center and a circle or a point on the sphere.

Volume of Sphere

The volume of the sphere is defined as follows:

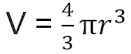
In this equation, "V" represents the volume and "r" represents the radius of the sphere.

Surface area of Sphere

In this equation, "A" represents the Surface area.

Spherical geometry

Dots and lines are fundamental elements of Euclidean plane geometry. On the field, the points are defined in the general sense. The analog of the "line" is Geodesic, which is a great circle; The defining feature of a great circle is that the plane with all its points also passes through the center of the sphere. Measuring the length of the arc shows that the shortest path between the two points on the sphere is the short segment of the great circle which contains the dots.

Many theorems from classical geometry are also true for spherical geometry, but not all do so because the field fails to satisfy some positions of classical geometry, including parallel geometry. In spherical trigonometry, angles are defined between great circles. Spherical trigonometry differs from normal trigonometry in many ways. For example, the sum of the interior angles of a circular triangle is always greater than 180 degrees. Also, any two equally spherical triangles are curved.